算数の入試問題には複数の解法が存在することが多い。もちろん得点するためには、そのすべての解法を思いつく必要はない。
しかし、複数の解法の中から最も最速で回答にたどりつける解法を思いつくことが大切だ。思いついた方法で解くしかないのだが、最速の方法を思いつけるような訓練をしておけば、初めて目にするような難問に取り組む余裕も生まれる。
具体例をあげて、最速の解法が真っ先にひらめくようになるためにはどうしたらよいかを解説していこう。

もくじ
問題で与えられた情報をダイレクトに使えないか検討する
上の問題は、正八角形の面積を求めるのではなく、図で色が塗られた部分、つまり正方形の四隅の直角二等辺三角形四個の面積と、正八角形の内側の四個の三角形の面積の合計を求めよというものである。
与えられらた数字は4cmという正八角形の中心と頂点の距離のみ。ダイレクトにこの数字を使うとはまさしく直感的なもので、理屈は後からついてくるものである。
算数の基本として足し算や掛け算がある。
まず、それを使ってみる。
4㎝という数字しかないので、それを2回掛けてみる。
すると正方形の面積の公式に思い当たる。
正方形の面積は基本中の基本だから、当たり前過ぎてこれが答えなのか疑ってしまうが、実はこれが正しい。とは言っても答えは4×4=16ではなく、その2倍の32だが。
4×4とはどの部分の面積なのか?
以下の図の通りである。
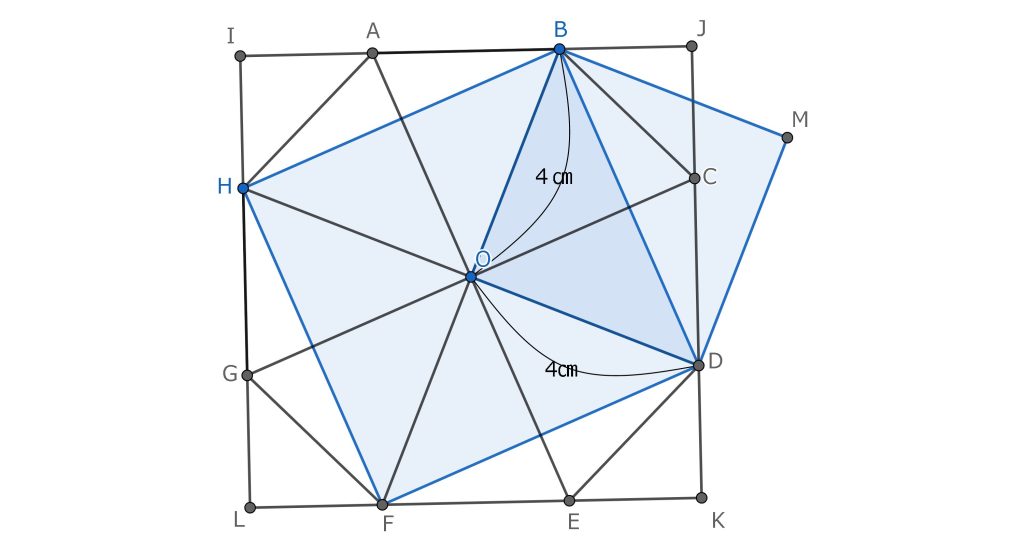
4×4は正方形OBMDの面積であるが、もとの正方形の内部で考えると、三角形BDHの面積と等しいことがわかる。直感的にこれでは、もとめる部分の面積には足りないことがわかるので、その2倍の正方形BDFHの面積が、問題で問われている部分の面積ではないかと気づくはず。

理由は後から考えればよい
このような問題では、直感力を信じることが重要で、最初に理屈を考えるとなかなか答えがでない。最初にひらめいた正方形の面積が答えである理由も一応書いておきますが、求められているのは答えで、理由ではありません。

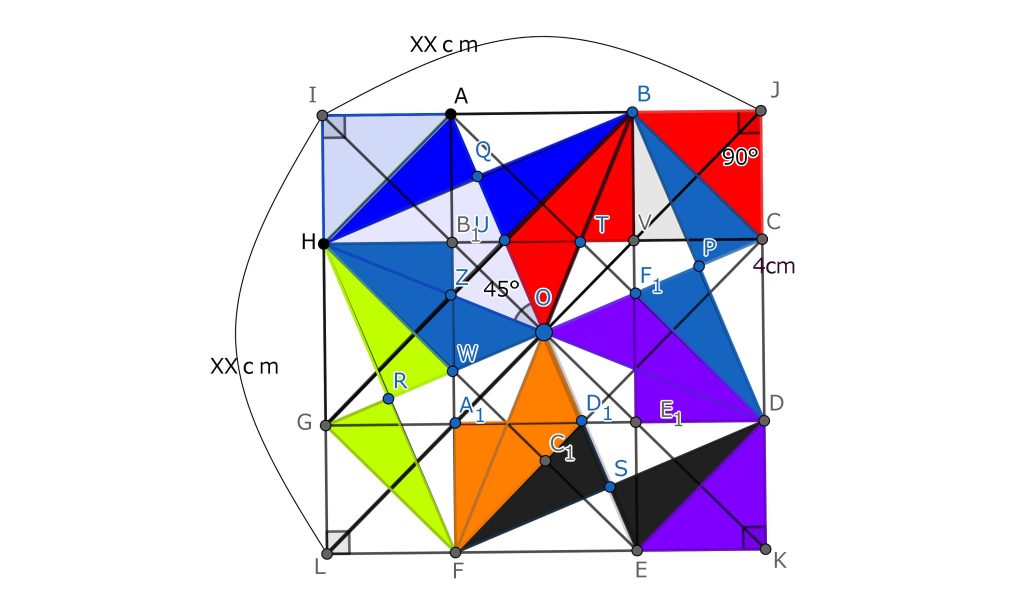
適当に垂線や平行線を引いて図形を分割して、移動すれば、最初に求めた正方形の面積に等しいことがわかる。要は直感が裏付けられたことになる。
4個の同じ図形が合わさったものだから、そのうちの一つ、例えば4角形AIHOについてみると、正方形BDFHからはみ出た部分AIHQは2つの三角形に分割される。三角形AIHとAHQの二つ。それぞれを移動して三角形BOQに当てはめたのが上の図である。
与えられている時間は少ない
問題を解くために与えられている時間は少ないのだから、答えの正しさの検証は後回しにすべきである。前のセクションに載せた図のような理由を考えていたら時間が足りなくなる人もおおいはずである。したがって、与えられた4という数字を使って何かの解答を記入してから、余った時間で理由を考えればよい。
正確な作図が正確な直感のひらめきにつながる。
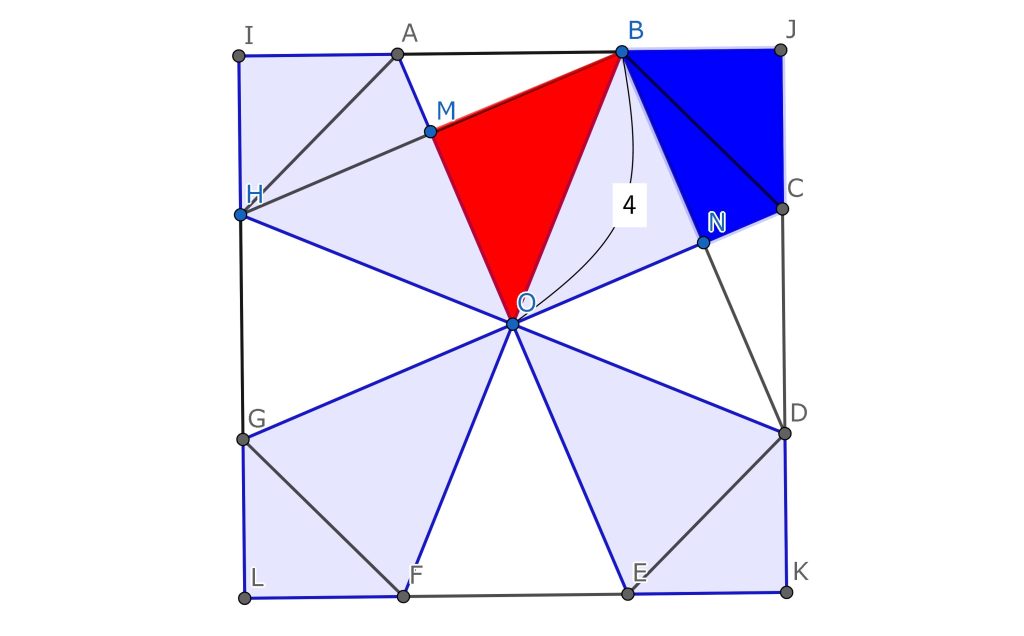
上の図は問題を正確に、単純に図示したものである。これを見て、「あーおそらく、青と赤の面積は同じなんだろうな」と気が付けばかなりの直感力があるといえる。
等しいとしたら、正方形BHFDの面積を求めれば、それがそのまま答えになる。理由は説明できなかったとしても、とりあえずそれを回答欄に書いておくことである。空欄が一番よくない。

コメント