発想の転換で簡単に！ドーナツ形面積の求め方とピタゴラス数の活用

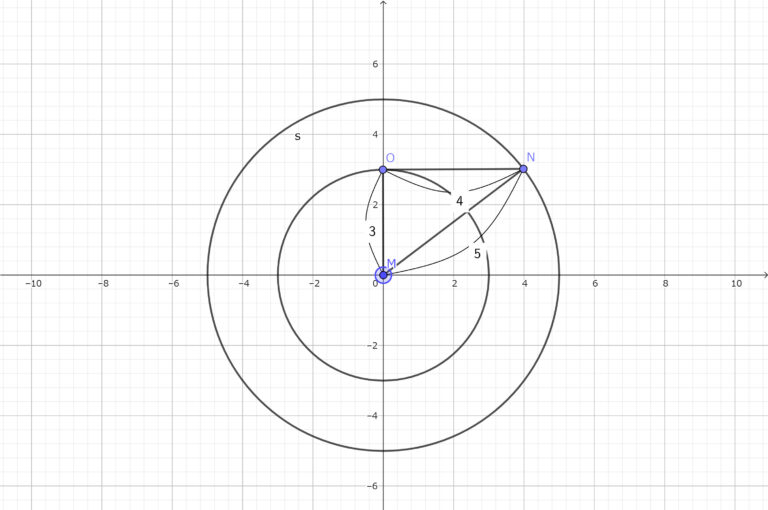
ドーナツ形の円の面積を求めよという問題をよく見かける。たとえば以下の図のような問題だ。

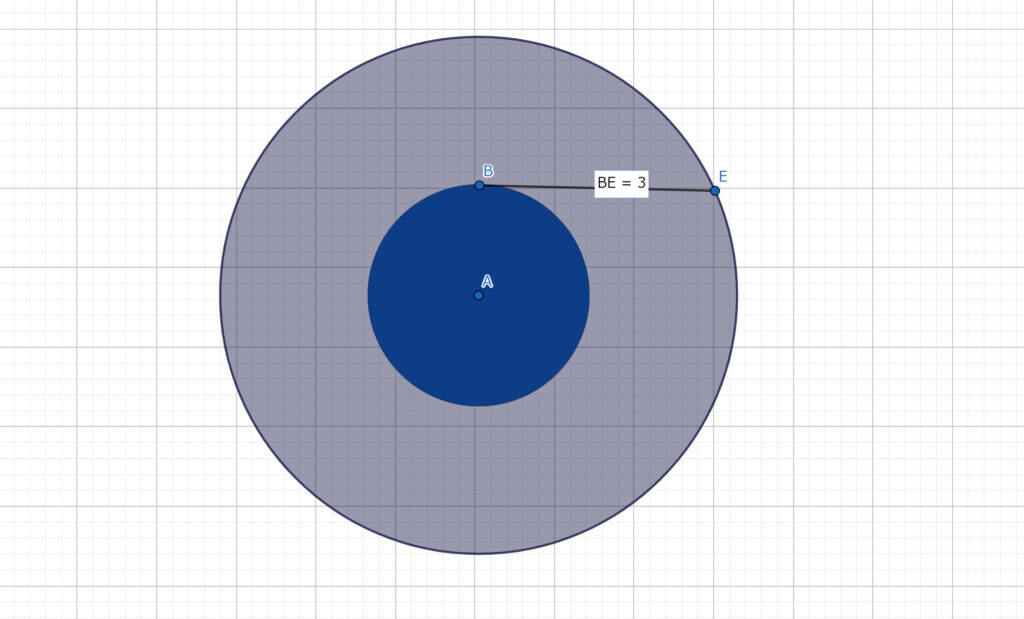
この問題は三平方の定理を使わないと解けなのだろうか？

ドーナツ型の面積に三平方の定理は必要ない

内側の小さい円の半径と、外側の大きな円の半径が分かれば、求めるのはその差だから、簡単そうにみえる。

だが、問題はその半径がどちらもわかっていないということ。大きな円の半径も、小さな円の半径もわからない。

実際、わからないのではなく、無数に存在するため、大きな円も小さな円も半径がわからないと言っている点が重要である。

小さな円と大きな円の面積の差が9㎠だったとしたら、大きな円が19㎠で小さな円が10㎠でも差は9㎠であるし、大きい円が20㎠で小さい円が11㎠でも面積の差、つまりドーナツ形の面積は9㎠である。こう考えると、答えは無数にあることになる。差が9である数の組み合わせはいくらでもある。

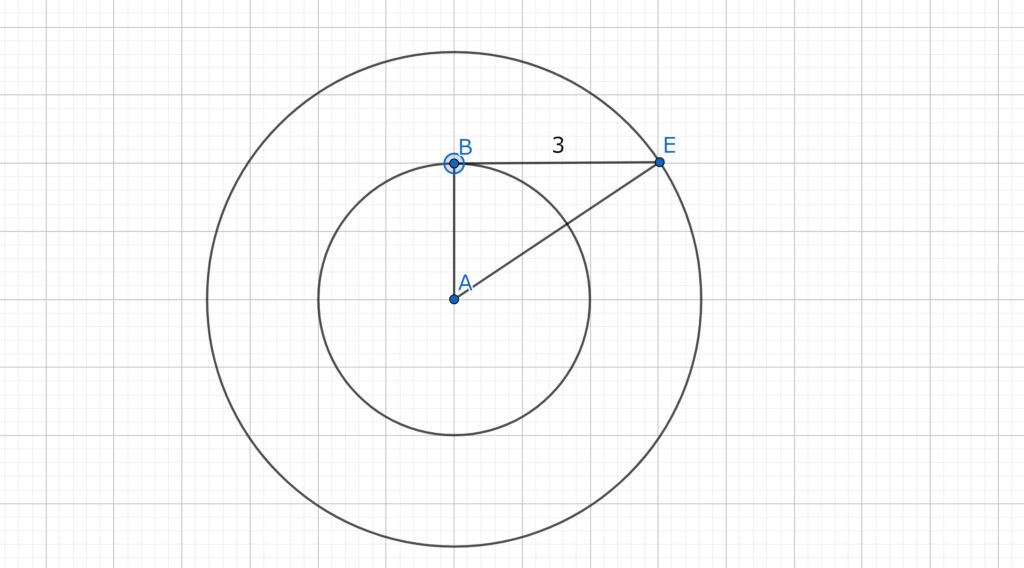
上の図を見て思いつくのは3対4対5の直角三角形ではないだろうか？

上の図には3センチの辺があるが、ほかの二辺の長さはわからだが、だが、3対4対5の直角三角形だったとしたらどうだろう？

当然大きな円が半径5センチ、小さな円が半径4センチとなる。上の図で、実際の長さはそのようになっていないはずである。

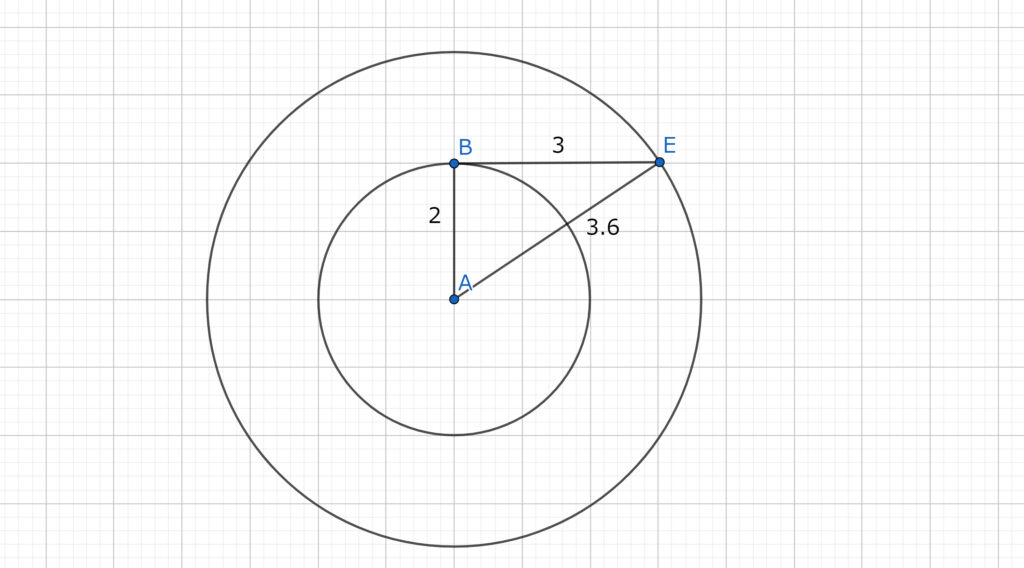
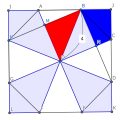
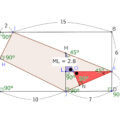
実際の長さはBAが2センチAEが約3.6センチなので、小さい円が2×２＝４で4π㎠。大きい円が3.6×3.6＝12.96π㎠｡なのでその差は約9㎠。便宜的に約といったが、正確に9㎠である。平方根を使わなかったのでその誤差がでただけ。

3対4対5の直角三角形を知っていれば、BEの長さが3ではなくても、比の考え方を使い、簡単に計算できる。

BEが2センチならそれぞれの辺を3分の2倍したものが、直角三角形の比となる。つまり、2:3分の8:3分の10の比になり、8/3×8/3＝64/9で、10/3×10/3＝100/9、その差は36/9＝4とな、2×2＝4と一致する。

どんな三角比の直角三角形をつかってもよい

例としてあげたのは、小学校でもならう3:4:5の直角三角形ですが、ほかにも (6:8:10) や (9:12:15) などの三組の自然数の組み合わせ(ピタゴラス数)は無限にあるので、√（平方根)無理数も含めればさらにある。1:√2：1の直角二等辺三角形などは、小学生でも知っている人は多いし、1を二回使っているので計算しやすい。

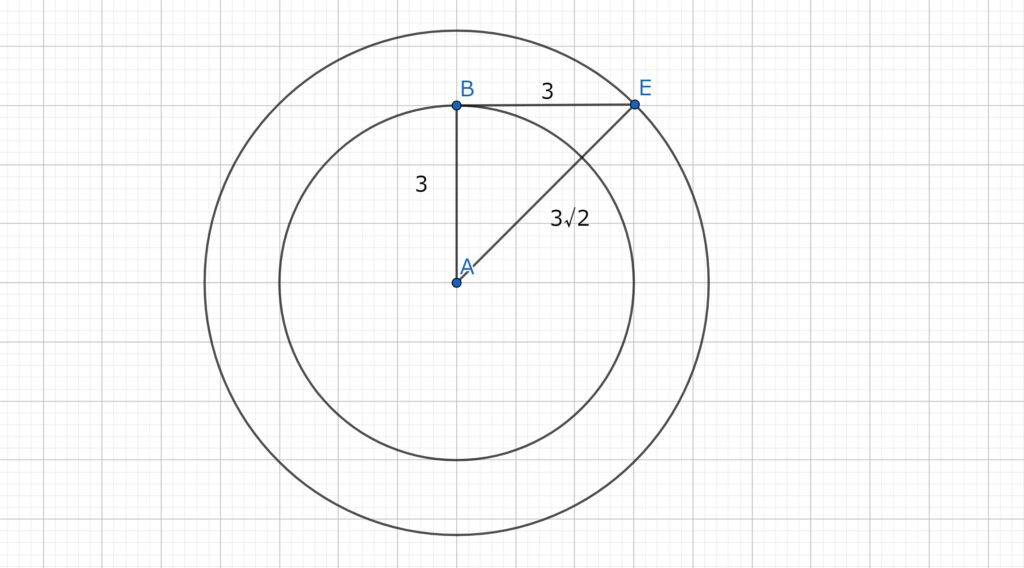
√が入っている直角三角形で最も単純な1：1：√２の図形を使っても簡単に計算できる。3×3＝９。３√2×3√２＝18。その差は9。やはり同じ結果となる。

三平方の定理を使って文字で置いたほうがわかりやすい時もある

大きな円の半径をラージRとし、小さい円の半径をスモールｒとして、三平方の定理をつかってBEの二乗はRの二乗－ｒの二乗とすれば容易に納得できるが、BEの二乗＋ｒの二乗＝Rの二乗を式変形して、この式、Rの二乗－ｒの二乗＝BEの二乗は導かれるが、√ルートや三平方の定理を知らなくてもドーナツ形の面積は簡単にだせるので、覚えておくと便利。

またこの感覚が三平方の定理の証明にもつながっていくので、あえて小学生の時期に三平方の定理や平方根は習わないほうが思考力や、洞察力、直観力が養われるだろう。