算数オリンピックといっても、基本的な知識があれば容易に解くことができる問題が出題されているのだが、なかなか中学生以上の数学を学んでいる人でも、解答にたどりつけないことが多い。そのような人の場合、自分の直観力にたいする注意力の欠如に問題の開放に気が付けない原因があることに気付く必要があるからだ。

上に載せた問題は算数オリンピックの問題だが、求められているのは色のついた部分の面積を求めよという至ってシンプルなことだ。
面積と言えば、長方形にせよ、正方形にせよ、縦×横だし、三角形もそれに掛ける二分の一がついただけである。
まず、その長方形や三角形の面積によってこの図形の四角形HIJKの面積は求められることに気付けばあとは簡単である。
もくじ
算数の問題は簡単なのになぜ解けないのか?
簡単なのに解けないといことはよくあるが、結局簡単なことを使いこなせていないことがその原因である。
まず、この図形から簡単にわかることは、三角形AHIと三角形CHJが同じ形であるということ。であれば、大きさが違っても、三角形、ここでは直角三角形の三辺の比は同じだということ。
左上の2:4の三角形の比は、簡単にすれば、1:2。ならば三角形CHJの対応する辺の比も同じなので、CH:CJ=1:2とわかる。この比が簡単にわかるなら、なんとなくHJと平行に見える辺IKを斜辺にもつ三角形BIKの辺の比を求められれば回答に一気に近づけると気づく。
ならば、それを求めにいくべきである。
BI:BKの辺の比は?HJとIKが平行ならば、辺の比も同じなのだが、直角記号がないので微妙に平行ではないのだろうと気づいた時点で、45度の記号に気付く。
45度と言えば、思いつくのは直角二等辺三角形である。
しかし、図形の中に直角二等辺三角形はない。ない場合は、自分でつくればよいだけ。

なんとなく、上の図のように補助線を引いてみると相似というか、同じ形の三角形が45度を二等分しているようにも見えるが、先ほど確認した通り、HJとIKが平行ではないので、二等分しているわけではない。
そこで以下のようにもう一本補助線を追加。
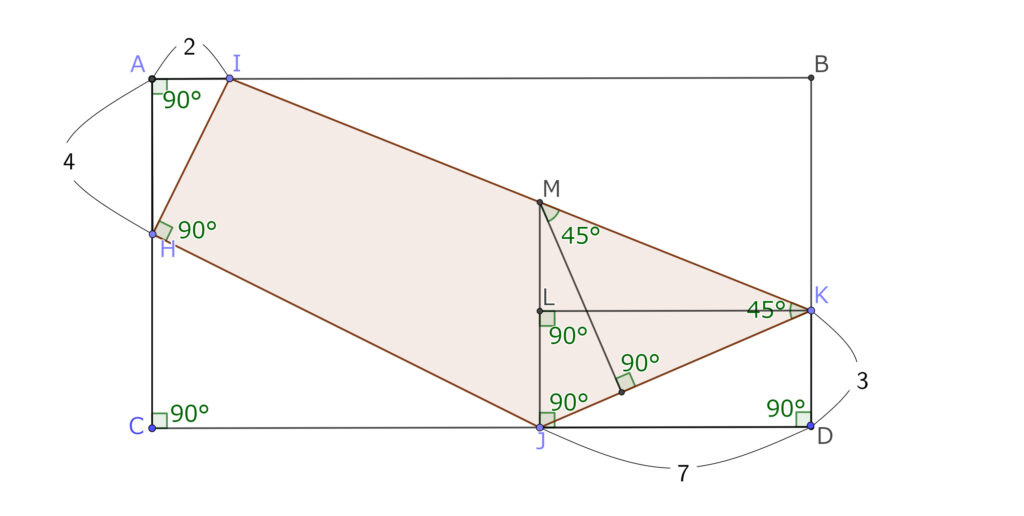
45度に対してもう一個45度を作ることで、一気に視野が広がる。
同じ形、いわゆる相似な直角三角形がいくつか現れていることに気付く。直角以外の同じ角度を共有している直角三角形は相似である。
連鎖的にみつかる相似な三角形
求めたい長さがわかっていても、ワンステップではそこに行けないことが多いので、何段階かステップを踏んでいく。
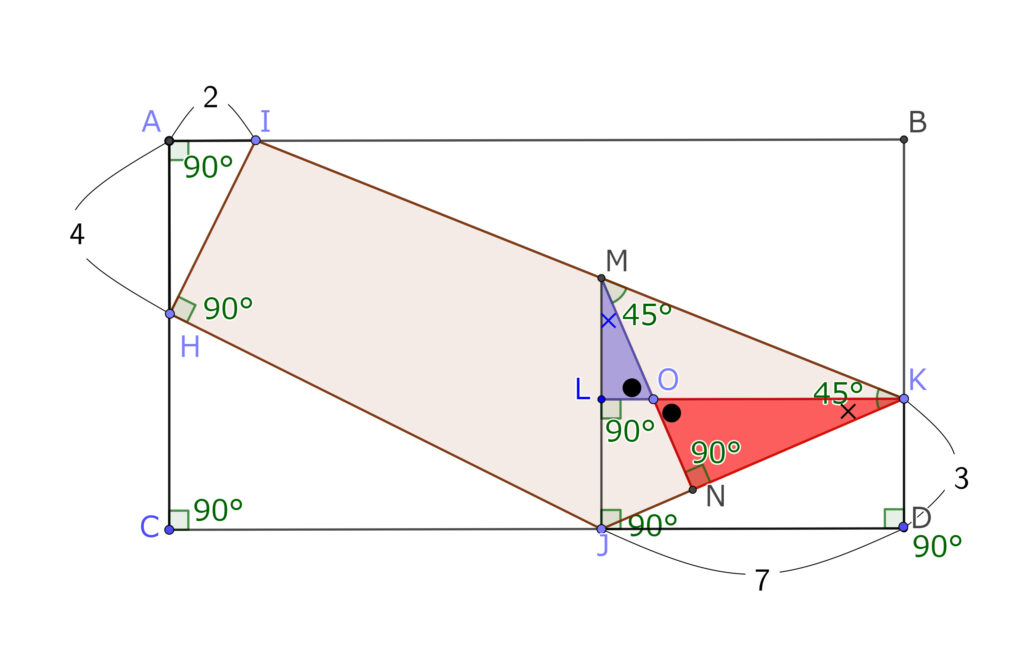
このように直角以外の同じ角度にしるしをつけると、同じ形、相似な直角三角形はすぐにみつかる。そして、最終的にMLの長さがわかれば、ML:LKの比がわかり、三角形BIKのBK:BIの比もわかりそうである。
三角形JKLは比がわかっているDJKをひっくり返したものだから、比も大きさも同じ、よって、LK=7LJ=3。この長さがわかっている三角形との関係で連鎖的に求める。
三角形KNOと三角形JKLは共に直角三角形で、一つの角度×で表した、角LKJを共有しているので、相似。直角をはさむ長い辺と短い辺の比は7:3。といことは辺KNの7分の3が辺NOにあたる。
この直角二等辺三角形の斜辺のKNは長さがわからないので、とりあえずXとおくと、その7分の3が辺NOになるので、NO=7分の3Xとなり、MN=KNなのでKNもX。Xから7分の3Xを引くと7分の4Xとなる。
長さがはっきりわかっている三角形を基準に連鎖させていくと、次は長さがわかっている三角形JKLと三角形JMNの相似の関係を利用することになる。
結局先ほどと同じことで、7:3の関係、MN:JNもMN×7分の3がJNになる。MNはXとおいているから7分の3Xとなり、MO,ON,JNという3辺の比が出た。7分の4:7分の3:7分の3。つまり。4:3:3とでる。
MNは直角二等辺三角形の斜辺だから、MN=KNで、MN =MO+ONだから、KN:NJは4+3:3で、7:3。
ある程度まで求めたら、いったん情報を整理する。
全段落で行ったことは簡単なのだが、文字であらわすと理解しづらい場合があるので、判明した情報をもとに、図を清書しておくのがより一層正答率があがる。
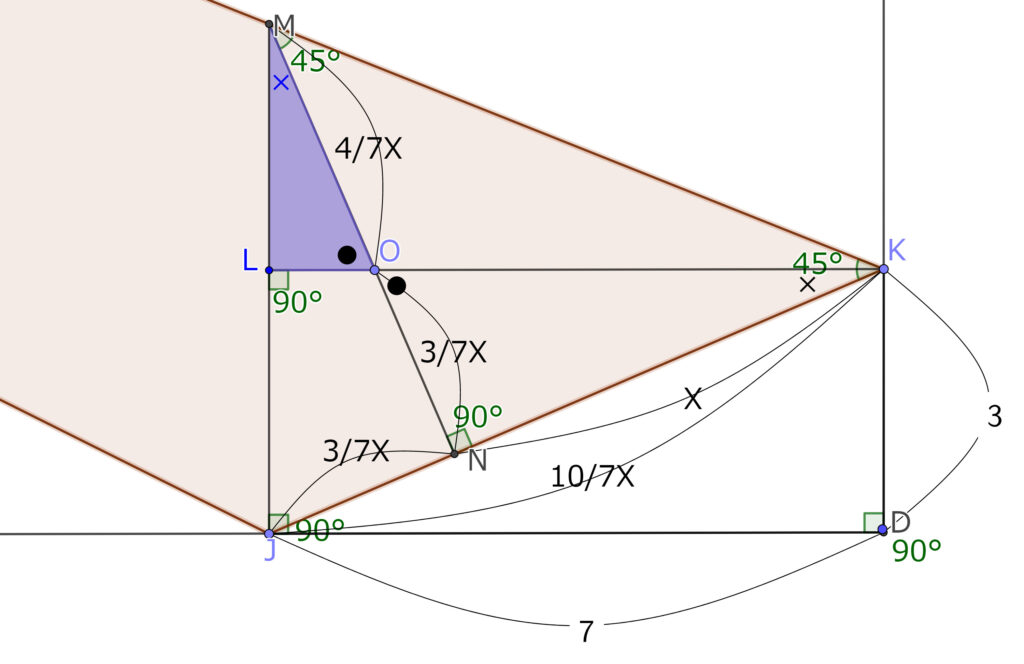
ここまで比が出そろうと、目的の数字まであと一歩だが、ここでも相似を使う。
三角形JKLと三角形LMOの相似の関係は、斜辺どうしを比べると、求めた比により7分の10:7分の4となり、簡単に表せば、10:4、さらに簡単にすると5:2となる。
直角をはさむ長いほうの辺は長さがわかっている7を使うと、辺MLの長さは、7×5分の2で求まる。7×2/5=14/5。
つまり、2.8となる。
下半分の三角形は7:3だったが、上半分は7:2.8だから、見た目には同じに見えたのも無理はない。
比から長さが求まったら、また比に戻って考える。
MLの長さが2.8と求まったので、直角をはさむ辺の比は7:2.8、少数だと扱いづらいので整数に直すと、とりあえず、10倍して、70:28これを、簡単にして、14で割ると5:2となる。
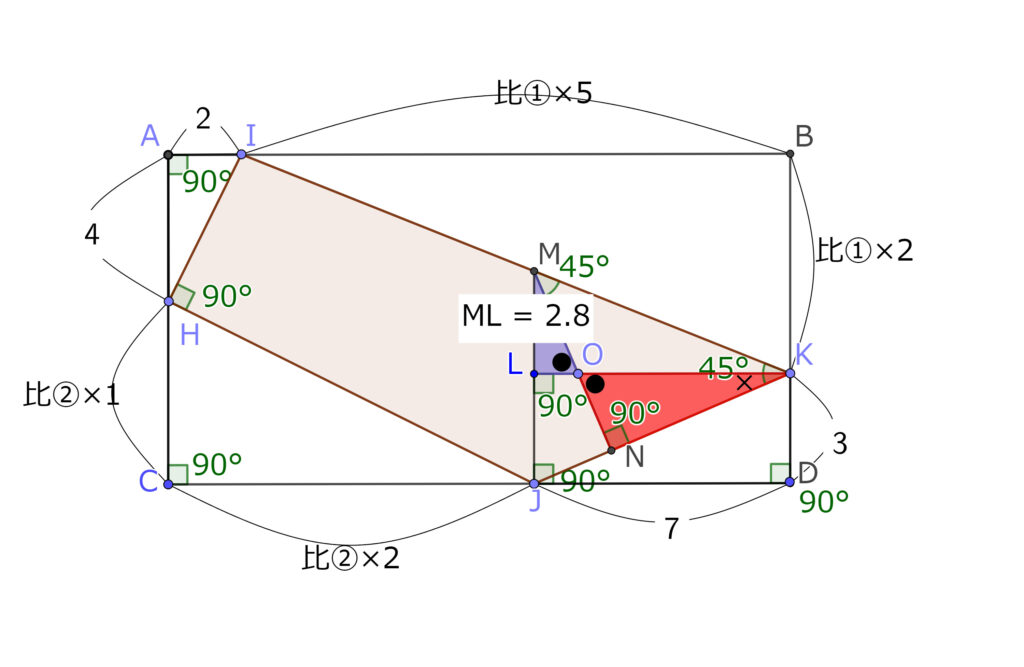
ML:LKが2:5ということは、辺MK、すなわち、辺IKの傾きが右に5行って2下がるという傾きだということ。だから辺IBの傾きは5分の2となる。
比の計算では比の値1がどのくらいなのかわからないので、とりあえず①とおくと、IB:BKは①×5:①×2となる。
最初からわかっていたように、左下の三角形の比は1:2なので、比の値1を②とおくとHC:HJは②×1:②×2となる。
少しは方程式のようなことも要求されることに注意
比がわかっても、求めるのは実際の値なので、すこし方程式のような計算が必要になるので、そこにも注意が必要である。
左上の辺AI2から順番に足していくと、2+①×5が長方形の横の長さ。
そこから7を引くと、長方形の下の辺CJがでる。そして、その半分が長方形の右側の辺①×2+3から左側の辺AH=4を引いたものに等しい。
式で表すと、(2+①×5-7)÷2=①×2+3‐4となる。
両辺に2をかけると、2+①×5-7=①×4+6-8となる。
計算できるところは計算してしまう。
①×5-5=①×4-2
①×5-①×4=3
①=3
比の値1が3と出たのだから、図に表すと以下の通り。
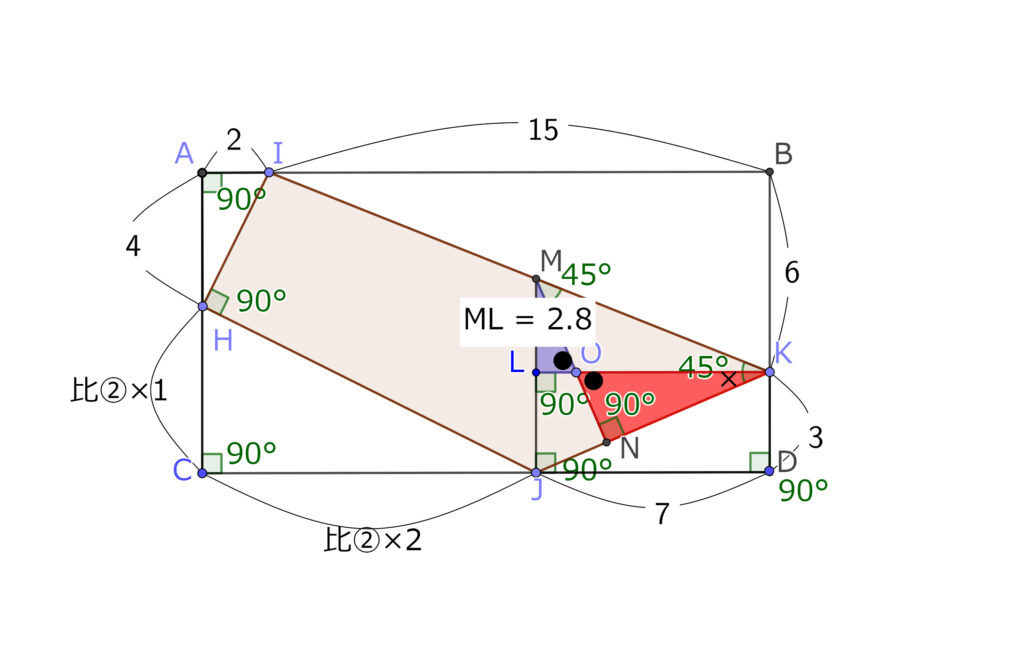
ここまで、わかると比の値②が5であることは容易にわかる。
最終的な答えは、掛け算、足し算と引き算で求める。
算数オリンピックといっても最終的には足し算、掛け算、引き算である。
長方形の面積は17×9で153。
周囲の三角形の面積はそれぞれ、左上から、2×4÷2=4、15×6÷2=45、3×7÷2=10.5、10×5÷2=25だから、
153-4+45+10.5+25=68.5
答え 68.5㎠
となる。
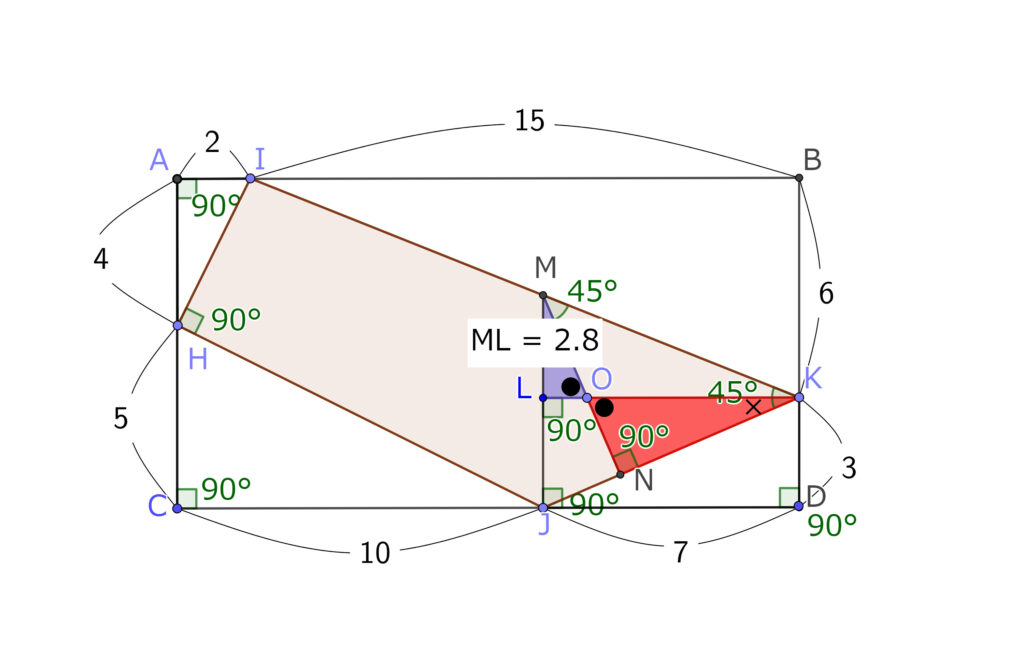
解答のプロセスは長いように見えるが、答えは意外と単純であることが多い、左下の三角形の斜辺の傾きが0.5なら、右上の三角形はそれより、少し緩い傾斜だなと感じるのなら、0.4かなと思って解いてみるのもアリだと思う。実際傾きは0.4で正解なのだから、わからなかったらきりのいい数字で検討をつけてそれをもとに解いていると、思いのほか正しかったりする。あきらめずに、直観を働かせ、それを信じることが正答への第一段階だといえる。
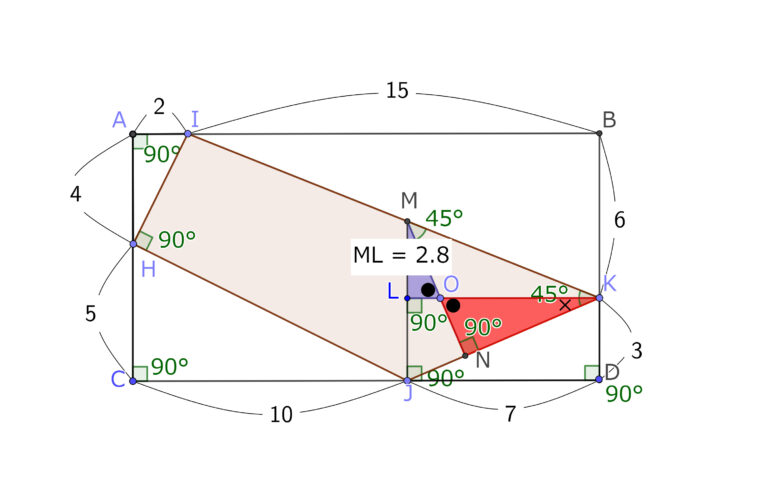

コメント